5月8日午後4時から、中学校超数学講座第3回が実施されました。

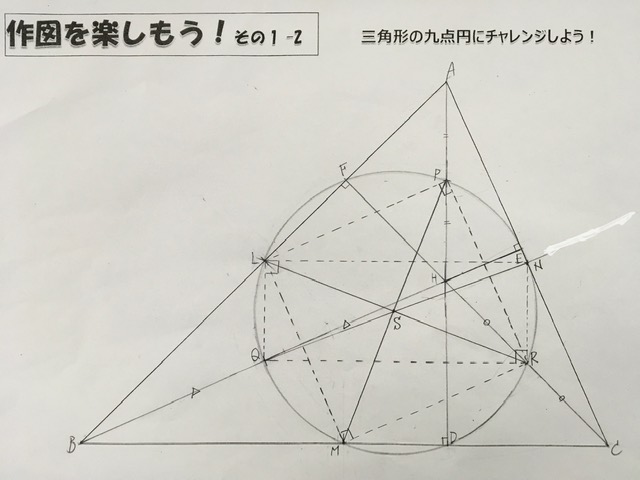
今回は「作図を楽しもう」の第2回目で、写真にあるように、「九点円にチャレンジしよう」
「円に内接する正五角形を作図しよう」
という作図に取り組みました。
まず九点円ですが、どんな三角形にもある円で、次の九点を通る円なのです。
・3辺の中点（図のM，N，L）

・頂点から対辺に下ろした垂線の足（図のD，E，F）

・垂心Hと3頂点の中点（図のP，Q，R）

それぞれコンパスと定規を用いて、作図していかなければなりませんので、皆四苦八苦して
点を取っていました。
そして、最後に九点を通る円を描くときも、なかなかうまく通らなかったりして、大変でしたが、
完成したときは感動の声が上がっていました。
それからどうして九点を通るのか、その中心はどこにあるのか、などの証明について考えました。
特に３年生は、最近学習した「中点連結の定理」や「円周角の性質」が利用されるので、興味深く
学んでいました。
「円に内接する正五角形」の作図も指示されたように描き、感心していました。
3年生には、「なぜこの作図で正五角形ができるのか」を考えてくることが宿題として出されました。
今回も「図形の奥の深さ」を味わう貴重な時間を過ごしました。

• 
• 
•