11月6日4限目、3年1組の「数学テーマ別課題発表会」を実施しました。
今回は、「平面図形の定理である、①中線定理 ②メネラウスの定理 ③チェバの定理 ④方べきの定理 ⑤トレミーの定理 ⑥シムソンの定理 の中から2つを選んで、その定理の証明とその定理がどのような図形の問題で応用されているのか、をレポートする」という課題でした。
「高校数学A」で今後学習予定の「図形の性質」の内容を先取りする課題ですので、なかなかむずかしかったと思います。
25名のレポートの中から、内容のすぐれているもの、ユニークな発想があるもの、まだ学習していない公式も思い切って採用し取り組んでいるもの、定理を使って応用問題がわかりやすく解かれているものなどの基準で選考し、発表する6人が選ばれました。
発表者は、「①と⑤」が2人、「②と③」が1人、「②と⑤」が1人、「③と⑤」が1人、「②と④」が1人という内訳でした。
皆、テレビに映し出される自分のレポートを説明しながら、定理に迫るプレゼンテーションをしました。
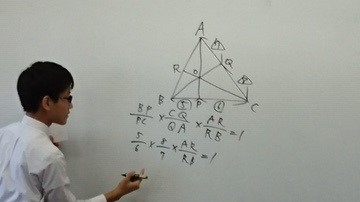
中には、ホワイトボードに定理を書き、その証明だけでなく、その定理の覚え方までわかりやすく解説する生徒もいました。
また定理が生まれた歴史的背景に触れる生徒もいました。
「トレミーの定理」が一番人気でした。
皆、どちらかというと図形が好きな生徒が多いので、発表には集中して聴き入っていました。
現在、「高校数学 Ⅰ」の「図形と三角比」の学習が終わったところです。
さらに図形への興味・関心を深め、将来の学習に向けて探究を深めてほしいと思います。
関連記事RECOMMEND
-
中学校
 2020.02.06 探究学習・STEAM
2020.02.06 探究学習・STEAM本年度最終、数学テーマ別課題発表会~3年1組~
-
中・高
 2020.12.09 探究学習・STEAM
2020.12.09 探究学習・STEAMSTEAM教育(探究学習)研修会(教職員)を実施しました。
-
高等学校
 2022.07.16 探究学習・STEAM
2022.07.16 探究学習・STEAMiCeMSキャラバン「学びのカラクリ」を実施しました。
-
中学校
 2020.10.29 探究学習・STEAM
2020.10.29 探究学習・STEAM10月28日放課後「第8回 中学校超数学講座」が実施されました。
-
中学校
 2021.04.17 地球学
2021.04.17 地球学「図書館ガイダンス及び新聞を活用した情報収集について」を実施しました。
-
高等学校
 2016.10.28 学校行事
2016.10.28 学校行事出前授業「年金セミナー」を実施しました。