2月15日2限、1月28日の2年1組に続いて、1年1組で「数学冬休みテーマ別宿題発表会」が行われました。
1年1組に課せられた「テーマ別宿題」のテーマは「円周率π」です。

～「円周率」とはどんな数なのか？　それは，3.1415926535………　　とどこまでも続く数であるという。どのようにしてそれがわかってきたかを，調べてきてほしい。
本でいろいろと調べてもよい。実験をしてもよい。解答をレポート用紙にまとめて書いて提出すること。～
以上が、生徒の皆さんに課せられたミッションです。1年1組の皆さんは、冬休みにいろいろと調べて、奮闘してレポートを作成しました。

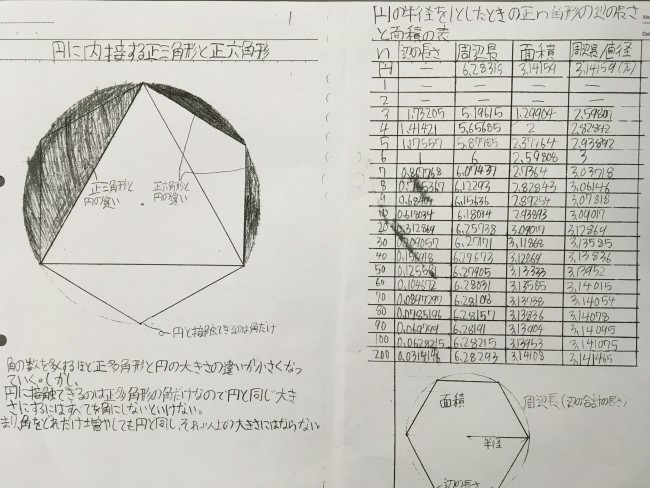
その中から優秀な4つのレポートが選出され（ノミネート）、15日の発表となりました。写真はそのレポートのうちの一部ですが、円に内接する正多角形の周の長さと面積から円周率を計算していく方法や，円の面積を正方形の面積に近似して円周率に近い値を計算する方法など、数学の歴史と深く関わってきたことを紹介しています。円周率の小数点以下の小さな数をどうやって正確に求めているのか？→「正多角形によるはさみうち」というむずかしい内容にも触れていました。プレゼンテーションが終わった後は大きな拍手が起こりました。

今日も、先生に代わって生徒代表が、普段よく使っている円周率πに関する授業をおこなったことにより、生徒の皆さんの数学への関心がますます高まったことと思います。